Soft Matter Physics Notes
Soft Matter Physic I
Notes about polymer physics, including key concepts and equations in soft matter physics. This document serves as a test for TeX equation practice and rendering.
单链构象
构象: 单键内旋转而产生的分子在空间中不同的形态。
静态柔顺性: $l_p=a*exp(\frac{\Delta \epsilon }{kT})$ 其中,$l_p$ 表示持续长度,$a$表示键长。
动态柔顺性: $\tau_p=\tau_0*exp(\frac{\Delta E}{kT})$ 其中,$\tau_p$ 表示持续时间。
均方末端距 $\langle\vec{R}^2\rangle$
自由连接链: $\langle\vec{R}^2\rangle _0=na^2$
自由旋转链: $\langle\vec{R}^2\rangle _{frc}=\frac{1+\cos\theta}{1-\cos\theta}\cdot na^2 \approx 2na^2$
受阻旋转链: $\langle\vec{R}^2\rangle _{hrc}=\frac{1+\cos\theta}{1-\cos\theta}\cdot \frac{1+\cos\varphi}{1-\cos\varphi}\cdot na^2$
令$\langle\vec{R}^2\rangle=C_{\infty}na^2$,其中$C_{\infty}$称为 Flory特征比
$R\sim \sqrt{n}a\sim n^{\nu}$,其中$\nu=\frac{1}{2}$
等效自由连接链(高斯链)
由$N$个长度为$b$的统计单元自由连接的分子链模型,与实际高分子由相同的均方末端距,$b$也叫 Kuhn length,$N=\frac{R_{max}^2}{C_{\infty}na^2}$,$b=\frac{\langle\vec{R}\rangle}{R_{max}}=\frac{C_{\infty}na^2}{R_{max}}$
假设: 分子链由$N$个链段组成,$N\gg1$;链段在空间中自由取向,随机行走,链段分布符合高斯分布。
理想链的自由能与熵弹性
聚合度为$N$,末端距为$\vec{R}$的概率密度分布函数为
\[P(N,\vec{R})=\Bigg( \frac{3}{2\pi Nb^2}\Bigg) ^{\frac{3}{2}} \cdot \exp \Bigg(-\frac{3\vec{R}^2}{2Nb^2} \Bigg) \tag{1}\]理想链的自由能为
\[F(N,\vec{R})=U(N,\vec{R})-T\cdot S(N,\vec{R}) \tag{2}\]由于理想链之间没有相互作用,$U(N,\vec{R})$为常数。
理想链的熵为
\[S(N,\vec{R})=k\ln \Omega(N,\vec{R}) \tag{3}\]已知 $P(N,\vec{R})=\frac{\Omega(N,\vec{R})}{\int \Omega(N,\vec{R}) \mathrm{d}\vec{R} }$,即
\[\Omega(N,\vec{R})=P(N,\vec{R})\cdot \int \Omega(N,\vec{R}) \mathrm{d}\vec{R} \tag{4}\]将上式代入(3)式,可得
\[\begin{aligned} S(N,\vec{R})&=k\ln\bigg[P(N,\vec{R})\cdot \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \\ &=k\ln [P(N,\vec{R})] + k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \end{aligned} \tag{5}\]将(1)式代入上式,又得
\[\begin{aligned} S(N,\vec{R})&=k\ln \Bigg[\Bigg( \frac{3}{2\pi Nb^2}\Bigg) ^{\frac{3}{2}} \cdot \exp \Bigg(-\frac{3\vec{R}^2}{2Nb^2} \Bigg) \Bigg]+k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \\ &=-\frac{3k}{2}\frac{\vec{R^2}}{Nb^2} + \frac{3}{2}k\ln \big(\frac{3}{2\pi Nb^2}\big) + k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \end{aligned} \tag{6}\]后两项为常数项,则(6)式可以写为
\[S(N,\vec{R})=-\frac{3k}{2}\frac{\vec{R^2}}{Nb^2}+S(N,0) \tag{7}\]代入(2)式,则自由能可以写为
\[F(N,\vec{R})=\frac{3kT}{2}\frac{\vec{R^2}}{Nb^2}+F(N,0) \tag{8}\]上式对$\vec{R}$求偏导,可得
\[\vec{f}=\frac{\partial F(N,\vec{R})}{\partial \vec{R}}=\frac{3kT}{Nb^2}\vec{R} \tag{9}\]由上式可以看到理想链表现为弹簧弹性,其弹性系数为$\frac{3kT}{Nb^2}$
均方回转半径
均方回转半径定义为 $\langle R_g^2\rangle=\frac{1}{n}\sum_{i=1}^n \langle (\vec{r}i-\vec{r}{cm})^2\rangle$
在统计上,当 $N\gg1$ ,且为自由连接链时,均方回转半径为均方末端距的 $\frac{1}{6}$ ,即
\[\langle R_g^2\rangle=\frac{Nb^2}{6}=\frac{\langle R^2 \rangle}{6} \tag{10}\]光散射实验
散射波矢 $q=\frac{4\pi}{\lambda}\sin\frac{\theta}{2}$
由Debye Function 导出 形状因子(Form Factor):
\[\vec{P}(q)=\frac{2N}{\big(q^2\langle R_g^2\rangle\big)^2}\bigg[ e^{-q^2\langle R_g^2\rangle}-1+q^2\langle R_g^2\rangle \bigg] \tag{11}\]小角散射
在小角散射实验中 $qR_g<1$,由Taylor展开式,$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+…$
则(11)式可以写成
\[\begin{aligned} \vec{P}(q)&=\frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\bigg[1-q^2\langle R_g^2\rangle+\frac{1}{2}\big(q^2\langle R_g^2\rangle \big)^2-\frac{1}{6}\big(q^2\langle R_g^2\rangle \big)^3-1+q^2\langle R_g^2\rangle \bigg]\\ &\simeq \frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\bigg[\frac{1}{2}\big(q^2\langle R_g^2\rangle \big)^2-\frac{1}{6}\big(q^2\langle R_g^2\rangle \big)^3 \bigg]\\ &=N-\frac{1}{3}N q^2\langle R_g^2\rangle \end{aligned}\]即
\[\begin{aligned} \vec{P}(q)&=N\left(1-\frac{q^2\langle R_g^2\rangle}{3}+\cdots \right)\\ &\simeq N\left(1-\frac{q^2\langle R_g^2\rangle}{3}\right) \end{aligned} \tag{12}\]对上式取倒数,得
\[\frac{1}{\vec{P}(q)}=\frac{1}{N}\cdot \frac{1}{1-\frac{q^2\langle R_g^2\rangle}{3}}\tag{13}\]对(13)式进行Taylor展开,$\frac{1}{1-x}=1+x+x^2+x^3+…$,可得
\[\frac{1}{I(q)}\sim \frac{1}{\vec{P}(q)}=\frac{1}{N}\cdot \bigg(1+\frac{q^2\langle R_g^2\rangle}{3} \bigg)\tag{14}\]小角散射实验中,对 $\frac{1}{I(q)}-q^2$ 作图,线性拟合后直线 斜率 为 $\frac{R_g^2}{3N}$,截距 为 $\frac{1}{N}$
广角散射
在广角散射实验中 $qR_g>1$,此时 $e^{-q^2\langle R_g^2\rangle}-1$可忽略,则(11)式可化简
\[\begin{split} \vec{P}(q)&\simeq \frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\cdot q^2\langle R_g^2\rangle \\ &=\frac{2N}{q^2\langle R_g^2\rangle} \end{split}\]对于理想链,将(10)式的均方回转半径和均方末端距关系代入上式,得
\[I(q)\sim \vec{P}(q)\simeq \frac{2N}{q^2\langle R_g^2\rangle}=\frac{12}{q^2 b^2}\sim \frac{1}{q^{1/\nu}}\tag{15}\]广角实验中,对 $\ln{I(q)}-\ln{q}$作图,线性拟合所得直线的 斜率 即为 $\nu$,对于实际聚合物分子链和理想链$\nu=\frac{1}{2}$
实际分子链与排除体积作用
排除体积(Excluded Volume): 长链分子的一部分不能占据另一部分分子所占据的空间。
排除体积参数:$\nu=(1-2\chi)l^3$
其中$\chi$为 Flory-Huggins参数
\[\chi\sim\epsilon_{AB}-\frac{1}{2}(\epsilon_{AA}-\epsilon_{BB})\tag{16}\]$\epsilon_{AB}$表示格子理论中,$AB$两种组分之间的相互作用能。
高分子链溶胀理论
高分子链和溶剂混合过程的自由能=理想链的自由能+排除体积的自由能,即
\[F=F_{idea}+F_{excluded}\tag{17}\]由(8)式可推得
\[\frac{F_{idea}}{kT}=\frac{3R^2}{2Nb^2}\tag{18}\]排除体积部分的自由能为
\[\frac{F_{excluded}}{kT}=\nu\bigg(\frac{N}{R^3}\bigg)^2R^3+\nu_3\bigg(\frac{N}{R^3}\bigg)^3R^3 \tag{19}\]其中$\big(\frac{N}{R^3}\big)^2$项表示两个单体出现在同一位置时的概率。
联立(17) - (18)式,可得
\[\frac{F}{kT}\sim \frac{3R^2}{2Nb^2}+\nu\bigg(\frac{N^2}{R^3}\bigg)+\nu_3\bigg(\frac{N^3}{R^6}\bigg)\tag{20}\]在 良溶剂 中(20)式最后一项可忽略,对$R$求偏导,得
\[\frac{\partial F}{\partial R}=\frac{3R}{Nb^2}-\frac{3\nu N^2}{R^4}\tag{21}\]令$\frac{\partial F}{\partial R}=0$ ,可得$3R^5=3\nu N^3b^2$,即
\[R_F\sim\nu^{\frac{1}{5}}\cdot N^{\frac{3}{5}} \tag{22}\]在 劣溶剂 中(20)的第一项可以忽略,同样对$R$求偏导,得
\[\frac{\partial F}{\partial R}=\nu\frac{N^2}{R^4}+\nu_3\frac{N^3}{R^6} \tag{23}\]令$\frac{\partial F}{\partial R}=0$ ,可得
\[R\sim\bigg(\frac{\nu_3}{\nu}\bigg)^\frac{1}{3}N^{\frac{1}{3}}\tag{24}\]在 $\theta$ 状态 时,除体积为0,此时的溶液叫做 $\theta$溶液,此时的温度为 $\theta$温度,由(15)式的实验中可以看到,高分子链尺寸$R$,与聚合度$N$的标度关系为 $\frac{1}{2}$,即
\[R=N^{\frac{1}{2}}\tag{25}\]对比(22)、(24)和(25)三种情况的标度关系可以看到不同的环境下,分子链的形貌尺寸也有差异,在良溶剂中,分子链舒展扩张,$\nu$较大,为$\frac{3}{5}$,在劣溶剂中,分子链收缩,$\nu$为$\frac{1}{3}$
链扩张因子(Chain Expansion Factor)$\alpha _s^2$
从$\theta$状态到良溶剂环境,分子链会发生溶胀扩张
\[\alpha _s^2=\frac{R_g^2}{R_{g,0}^2}\tag{26}\]其中${R_{g,0}^2}$表示$\theta$状态下的分子的均方回转半径,将标度关系代入上式,可得
\[\alpha _s^2=\frac{R_g^2}{R_{g,0}^2}\sim\frac{\big(N^{\frac{3}{5}}\big)^2}{\big(N^{\frac{1}{2}}\big)^2}=N^{\frac{1}{5}}\tag{27}\]真实链的稀溶液与Zimm Plot
浓度为$c$的高分子溶液,渗透压为
\[\frac{\Pi}{kT}=\frac{1}{M}c+A_2\cdot c^2+... \tag{28}\]其中,$M$为数均分子量,$A_2$表示第二维利系数,$A_2\sim\frac{R_g^3}{M^2}\sim N^{3\nu-2}$
将(28)式对$c$求偏导
\[\frac{\partial(\Pi/kT)}{\partial c}=\frac{1}{M}+2A_2\cdot c+... \tag{29}\]稀溶液中,忽略高次项,对$\frac{\partial(\Pi/kT)}{\partial c}-c$作图,线性拟合所得直线 斜率 为$2A_2$,截距 为$\frac{1}{M}$。
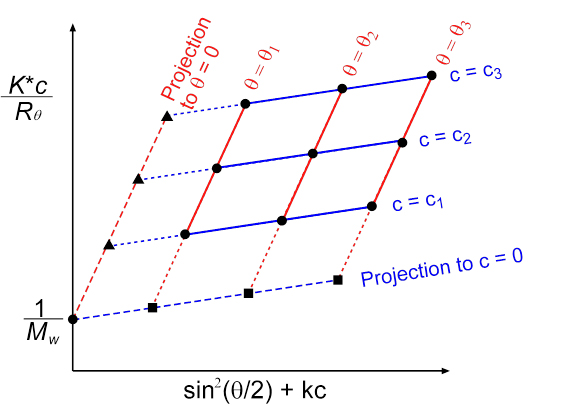
Zimm Plot 数据处理方法
-
方法一:固定散射角 $\theta$,改变浓度 $c$
- 在固定的 $\theta$ 下,测量不同浓度下的 $\frac{K\cdot c}{R_\theta}$。
- 作 $\frac{K\cdot c}{R_\theta}$ 对 $c$ 的图像,外推至 $c \to 0$,得到 $\big(\frac{K \cdot c}{R_\theta}\big)_{c\to0}$。
- 对所有不同的 $\theta$,重复上述步骤,得到一系列 $\big(\frac{K \cdot c}{R_\theta}\big)_{c\to0}$。
- 作 $\big(\frac{K \cdot c}{R_\theta}\big)_{c\to0}$ 对 $\sin^2\frac{\theta}{2}$ 的曲线,线性拟合:
- 截距:$\frac{1}{M_w}$
- 斜率:$\frac{16\pi^2 n^2}{3\lambda^2}\langle R_g^2\rangle$
-
方法二:固定浓度 $c$,改变散射角 $\theta$
- 在固定的 $c$ 下,测量不同 $\theta$ 下的 $\frac{K\cdot c}{R_\theta}$。
- 作 $\frac{K\cdot c}{R_\theta}$ 对 $\sin^2\frac{\theta}{2}$ 的图像,外推至 $\theta \to 0$,得到 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta\to0}$。
- 对所有不同的 $c$,重复上述步骤,得到一系列 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta\to0}$。
- 作 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta\to0}$ 对 $c$ 的曲线,线性拟合:
- 截距:$\frac{1}{M_w}$
- 斜率:$2A_2$
通过上述两种方法,可以分别获得高分子的重均分子量 $M_w$、均方回转半径 $\langle R_g^2\rangle$ 以及第二维利系数 $A_2$,从而全面表征高分子的结构与溶液性质。
共混与溶液动力学:格子理论
理想气体的混合过程
理想气体模型将气体分子看作质点(有质量、无体积),分子间没有相互作用,严格遵循气体状态方程。
两种理想气体 $AB$ 在温度 $T$,压强 $p$ 下混合,混合过程的熵变为
\[\Delta S=\Delta S_A+\Delta S_B=n_AR\ln\frac{V_A+V_B}{V_A}+n_BR\ln\frac{V_A+V_B}{V_B}\tag{31}\]其中,$n_A$ 表示 $A$ 组分的物质的量,$V_A$表示 $A$ 组分的体积,由摩尔分数的关系 $x_A=\frac{n_A}{n_A+n_B}$ 代换上式,可得
\[\Delta S_{mix}=-nR(x_A\ln x_A+x_B\ln x_B) \tag{32}\]由于是理想气体,分子之间无相互作用,则
\[\Delta H_{mix}=0 \tag{33}\]由此可得理想气体混合过程的吉布斯自由能变为
\[\Delta G_{mix}=\Delta H_{mix}-T\Delta S_{mix}=nRT(x_A\ln x_A+x_B\ln x_B)\tag{34}\]理想溶液混合过程
理想溶液中各组分分子之间相互作用相同,溶质分子与溶剂分子混合时,无热效应,无体积变化,即 $\epsilon_{AA}=\epsilon_{BB}=\epsilon_{AB}$

将理想气体中的摩尔分数换为体积分数,即
\[\phi_A=\frac{n_A}{n_A+n_B}=x_A\]混合前,$AB$ 组分状态数量为1,熵为0
\[S_0^A=S_0^B=k\ln 1=0\tag{35}\]混合后
\[\Delta S_{f}=k\ln \Omega=-k[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\tag{36}\]则混合过程的熵变为
\[\begin{aligned} \Delta S_{mix}&=-k[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\\ &=-k[n_A\ln\phi_A+n_B\ln\phi_B] \end{aligned} \tag{37}\]由于是理想液体,混合过程焓变为0,则混合过程的吉布斯自由能变为
\[\Delta G_{mix}=nkT[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\tag{38}\]实际溶液的混合过程
实际溶液混合过程能量变化不可忽略
混合过程由格子理论易推得
\[\Delta E_{mix}=\frac{zn}{2}\phi_A\phi_B(2\epsilon_{AB}-\epsilon_{AA}-\epsilon_{BB})\tag{39}\]其中$z$表示配位数,定义Folry-Huggins参数
\[\chi\equiv\frac{z}{2kT}((2\epsilon_{AB}-\epsilon_{AA}-\epsilon_{BB}))\tag{40}\]则(39)式可以写为
\[E_{mix}=nkT\chi \phi_A \phi_B\tag{41}\]- 当 $\chi<0$ 时,溶质倾向于溶解于溶剂中
- 当 $\chi>0$ 时,倾向于分相,即不溶解
- 当 $\chi=0$ 时,表现为理想溶液的特点
实际溶液混合过程中熵变与理想溶液一致,则混合过程的自由能变为
\[\Delta F_{mix}=\Delta E_{mix}-T\Delta S_{mix}=nkT[\phi_A\ln\phi_A+\phi_B\ln\phi_B+\chi\phi_A\phi_B]\tag{42}\]高分子溶液与高分子共混
高分子共混中,每条分子链的自由能为
\[\frac{\Delta F_{mix}}{n/N}=kT[\phi_A\ln\phi_A+\phi_B\ln\phi_B+\chi N\phi_A\phi_B]\tag{43}\]高分子溶液中,每个格点的自由能变化为
\[\frac{\Delta F_{mix}}{n}=kT[\frac{\phi_A}{N_A}\ln\phi_A+\phi_B\ln\phi_B+\chi\phi_A\phi_B]\tag{44}\]