Soft Matter Physic I

单链构象

构象： 单键内旋转而产生的分子在空间中不同的形态。

静态柔顺性： $l_p=a*exp(\frac{\Delta \epsilon }{kT})$ 其中，$l_p$ 表示持续长度，$a$表示键长。

动态柔顺性： $\tau_p=\tau_0*exp(\frac{\Delta E}{kT})$ 其中，$\tau_p$ 表示持续时间。

均方末端距 $\langle\vec{R}^2\rangle$

自由连接链： $\langle\vec{R}^2\rangle _0=na^2$

自由旋转链： $\langle\vec{R}^2\rangle _{frc}=\frac{1+\cos\theta}{1-\cos\theta}\cdot na^2 \approx 2na^2$

受阻旋转链： $\langle\vec{R}^2\rangle _{hrc}=\frac{1+\cos\theta}{1-\cos\theta}\cdot \frac{1+\cos\varphi}{1-\cos\varphi}\cdot na^2$

令$\langle\vec{R}^2\rangle=C_{\infty}na^2$,其中$C_{\infty}$称为 Flory特征比

$R\sim \sqrt{n}a\sim n^{\nu}$，其中$\nu=\frac{1}{2}$

等效自由连接链（高斯链）

由$N$个长度为$b$的统计单元自由连接的分子链模型，与实际高分子由相同的均方末端距，$b$也叫 Kuhn length，$N=\frac{R_{max}^2}{C_{\infty}na^2}$，$b=\frac{\langle\vec{R}\rangle}{R_{max}}=\frac{C_{\infty}na^2}{R_{max}}$

假设： 分子链由$N$个链段组成，$N\gg1$；链段在空间中自由取向，随机行走，链段分布符合高斯分布。

理想链的自由能与熵弹性

聚合度为$N$，末端距为$\vec{R}$的概率密度分布函数为

$$P(N,\vec{R})=\Bigg( \frac{3}{2\pi Nb^2}\Bigg) ^{\frac{3}{2}} \cdot \exp \Bigg(-\frac{3\vec{R}^2}{2Nb^2} \Bigg) \tag{1}$$

理想链的自由能为

$$F(N,\vec{R})=U(N,\vec{R})-T\cdot S(N,\vec{R}) \tag{2}$$

由于理想链之间没有相互作用，$U(N,\vec{R})$为常数。

理想链的熵为

$$S(N,\vec{R})=k\ln \Omega(N,\vec{R}) \tag{3}$$

已知 $P(N,\vec{R})=\frac{\Omega(N,\vec{R})}{\int \Omega(N,\vec{R}) \mathrm{d}\vec{R} }$，即

$$\Omega(N,\vec{R})=P(N,\vec{R})\cdot \int \Omega(N,\vec{R}) \mathrm{d}\vec{R} \tag{4}$$

将上式代入(3)式,可得

$$\begin{split} S(N,\vec{R})&=k\ln\bigg[P(N,\vec{R})\cdot \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \\ &=k\ln [P(N,\vec{R})] + k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \tag{5} \end{split}$$

将(1)式代入上式，又得

$$\begin{split} S(N,\vec{R})&=k\ln \Bigg[\Bigg( \frac{3}{2\pi Nb^2}\Bigg) ^{\frac{3}{2}} \cdot \exp \Bigg(-\frac{3\vec{R}^2}{2Nb^2} \Bigg) \Bigg]+k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \\ &=-\frac{3k}{2}\frac{\vec{R^2}}{Nb^2} + \frac{3}{2}k\ln \big(\frac{3}{2\pi Nb^2}\big) + k\ln \bigg[ \int \Omega(N,\vec{R}) \mathrm{d}\vec{R}\bigg] \tag{6} \end{split}$$

后两项为常数项，则(6)式可以写为

$$S(N,\vec{R})=-\frac{3k}{2}\frac{\vec{R^2}}{Nb^2}+S(N,0) \tag{7}$$

代入(2)式，则自由能可以写为

$$F(N,\vec{R})=\frac{3kT}{2}\frac{\vec{R^2}}{Nb^2}+F(N,0) \tag{8}$$

上式对$\vec{R}$求偏导，可得

$$\vec{f}=\frac{\partial F(N,\vec{R})}{\partial \vec{R}}=\frac{3kT}{Nb^2}\vec{R} \tag{9}$$

由上式可以看到理想链表现为弹簧弹性，其弹性系数为$\frac{3kT}{Nb^2}$

均方回转半径

$$\langle R_g^2\rangle=\frac{1}{n}\sum_{i=1}^n \langle (\vec{r}_i-\vec{r}_{cm})^2\rangle$$

在统计上，当$N\gg1$，且为自由连接链时，均方回转半径为均方末端距的$\frac{1}{6}$，即

$$\langle R_g^2\rangle=\frac{Nb^2}{6}=\frac{\langle R^2 \rangle}{6} \tag{10}$$

光散射实验

散射波矢 $q=\frac{4\pi}{\lambda}\sin\frac{\theta}{2}$

由Debye Function 导出 形状因子（Form Factor）:

$$\vec{P}(q)=\frac{2N}{\big(q^2\langle R_g^2\rangle\big)^2}\bigg[ e^{-q^2\langle R_g^2\rangle}-1+q^2\langle R_g^2\rangle \bigg] \tag{11}$$

小角散射

在小角散射实验中 $qR_g<1$，由Taylor展开式，$e^x=1+x+\frac{x^2}{2!}+\frac{x^3}{3!}+...$

则(11)式可以写成

$$\begin{split} \vec{P}(q)&=\frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\bigg[1-q^2\langle R_g^2\rangle+\frac{1}{2}\big(q^2\langle R_g^2\rangle \big)^2-\frac{1}{6}\big(q^2\langle R_g^2\rangle \big)^3-1+q^2\langle R_g^2\rangle \bigg]\\ &\simeq \frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\bigg[\frac{1}{2}\big(q^2\langle R_g^2\rangle \big)^2-\frac{1}{6}\big(q^2\langle R_g^2\rangle \big)^3 \bigg]\\ &=N-\frac{1}{3}N q^2\langle R_g^2\rangle \end{split}$$

即

$$\begin{split} \vec{P}(q)&=N\bigg(1-\frac{q^2\langle R_g^2\rangle}{3}+... \bigg)\\ &\simeq N\bigg(1-\frac{q^2\langle R_g^2\rangle}{3}\bigg) \tag{12} \end{split}$$

对上式取倒数，得

$$\frac{1}{\vec{P}(q)}=\frac{1}{N}\cdot \frac{1}{1-\frac{q^2\langle R_g^2\rangle}{3}}\tag{13}$$

对(13)式进行Taylor展开，$\frac{1}{1-x}=1+x+x^2+x^3+...，可得$

$$\frac{1}{I(q)}\sim \frac{1}{\vec{P}(q)}=\frac{1}{N}\cdot \bigg(1+\frac{q^2\langle R_g^2\rangle}{3} \bigg)\tag{14}$$

小角散射实验中，对 $\frac{1}{I(q)}-q^2$ 作图，线性拟合后直线 斜率 为 $\frac{R_g^2}{3N}$，截距 为 $\frac{1}{N}$

广角散射

在广角散射实验中 $qR_g>1$，此时 $e^{-q^2\langle R_g^2\rangle}-1$可忽略，则(11)式可化简

$$\begin{split} \vec{P}(q)&\simeq \frac{2N}{\big(q^2\langle R_g^2\rangle \big)^2}\cdot q^2\langle R_g^2\rangle \\ &=\frac{2N}{q^2\langle R_g^2\rangle} \end{split}$$

对于理想链，将(10)式的均方回转半径和均方末端距关系代入上式，得

$$I(q)\sim \vec{P}(q)\simeq \frac{2N}{q^2\langle R_g^2\rangle}=\frac{12}{q^2 b^2}\sim \frac{1}{q^{1/\nu}}\tag{15}$$

广角实验中，对 $\ln{I(q)}-\ln{q}$作图，线性拟合所得直线的 斜率 即为 $\nu$，对于实际聚合物分子链和理想链$\nu=\frac{1}{2}$

实际分子链与排除体积作用

排除体积（Excluded Volume）： 长链分子的一部分不能占据另一部分分子所占据的空间。

排除体积参数：$\nu=(1-2\chi)l^3$

其中$\chi$为 Flory-Huggins参数

$$\chi\sim\epsilon_{AB}-\frac{1}{2}(\epsilon_{AA}-\epsilon_{BB})\tag{16}$$

$\epsilon_{AB}$表示格子理论中，$AB$两种组分之间的相互作用能。

高分子链溶胀理论

高分子链和溶剂混合过程的自由能=理想链的自由能+排除体积的自由能，即

$$F=F_{idea}+F_{excluded}\tag{17}$$

由(8)式可推得

$$\frac{F_{idea}}{kT}=\frac{3R^2}{2Nb^2}\tag{18}$$

排除体积部分的自由能为

$$\frac{F_{excluded}}{kT}=\nu\bigg(\frac{N}{R^3}\bigg)^2R^3+\nu_3\bigg(\frac{N}{R^3}\bigg)^3R^3 \tag{19}$$

其中$\big(\frac{N}{R^3}\big)^2$项表示两个单体出现在同一位置时的概率。

联立(17) - (18)式，可得

$$\frac{F}{kT}\sim \frac{3R^2}{2Nb^2}+\nu\bigg(\frac{N^2}{R^3}\bigg)+\nu_3\bigg(\frac{N^3}{R^6}\bigg)\tag{20}$$

在 良溶剂 中(20)式最后一项可忽略，对$R$求偏导，得

$$\frac{\partial F}{\partial R}=\frac{3R}{Nb^2}-\frac{3\nu N^2}{R^4}\tag{21}$$

令$\frac{\partial F}{\partial R}=0$ ，可得$3R^5=3\nu N^3b^2$，即

$$R_F\sim\nu^{\frac{1}{5}}\cdot N^{\frac{3}{5}} \tag{22}$$

在 劣溶剂 中(20)的第一项可以忽略，同样对$R$求偏导，得

$$\frac{\partial F}{\partial R}=\nu\frac{N^2}{R^4}+\nu_3\frac{N^3}{R^6} \tag{23}$$

令$\frac{\partial F}{\partial R}=0$ ，可得

$$R\sim\bigg(\frac{\nu_3}{\nu}\bigg)^\frac{1}{3}N^{\frac{1}{3}}\tag{24}$$

在 $\theta$ 状态 时，除体积为0，此时的溶液叫做 $\theta$溶液，此时的温度为 $\theta$温度，由(15)式的实验中可以看到，高分子链尺寸$R$，与聚合度$N$的标度关系为 $\frac{1}{2}$，即

$$R=N^{\frac{1}{2}}\tag{25}$$

对比(22)、(24)和(25)三种情况的标度关系可以看到不同的环境下，分子链的形貌尺寸也有差异，在良溶剂中，分子链舒展扩张，$\nu$较大，为$\frac{3}{5}$，在劣溶剂中，分子链收缩，$\nu$为$\frac{1}{3}$

链扩张因子（Chain Expansion Factor）$\alpha _s^2$

从$\theta$状态到良溶剂环境，分子链会发生溶胀扩张

$$\alpha _s^2=\frac{R_g^2}{R_{g,0}^2}\tag{26}$$

其中${R_{g,0}^2}$表示$\theta$状态下的分子的均方回转半径，将标度关系代入上式，可得

$$\alpha _s^2=\frac{R_g^2}{R_{g,0}^2}\sim\frac{\big(N^{\frac{3}{5}}\big)^2}{\big(N^{\frac{1}{2}}\big)^2}=N^{\frac{1}{5}}\tag{27}$$

真实链的稀溶液与Zimm Plot

浓度为$c$的高分子溶液，渗透压为

$$\frac{\Pi}{kT}=\frac{1}{M}c+A_2\cdot c^2+... \tag{28}$$

其中，$M$为数均分子量，$A_2$表示第二维利系数，$A_2\sim\frac{R_g^3}{M^2}\sim N^{3\nu-2}$

将(28)式对$c$求偏导

$$\frac{\partial(\Pi/kT)}{\partial c}=\frac{1}{M}+2A_2\cdot c+... \tag{29}$$

稀溶液中，忽略高次项，对$\frac{\partial(\Pi/kT)}{\partial c}-c$作图，线性拟合所得直线 斜率 为$2A_2$，截距 为$\frac{1}{M}$。

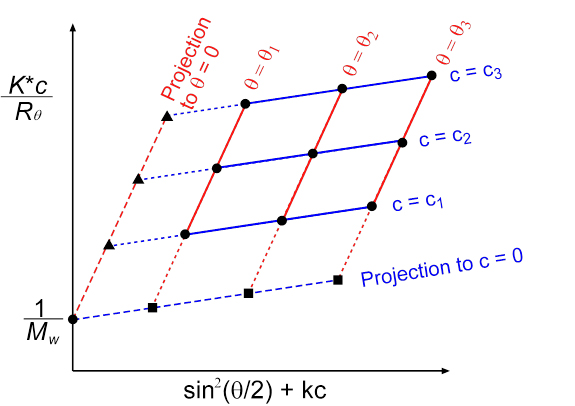
Zimm Plot

配置一系列不同浓度的溶液，测定各个溶液在不同散射角时的Rayleigh因子$R_\theta$

$$\frac{K\cdot c}{R_\theta}=\frac{1}{M_w}\bigg(1+\frac{16\pi^2n^2}{3\lambda^2}\langle R_g^2\rangle\sin^2{\frac{\theta}{2}}+...\bigg)+A_2\cdot c\tag{30}$$

其中，$K$为光学常数，$n$为溶液折射率，$R_\theta=r^2\frac{I_s}{I_0}$，表示散射光强。

• 将在固定的 $\theta$ 下所测得的 $\frac{K\cdot c}{R_\theta}$ 值随浓度变化作图，得 $\big(\frac{K \cdot c}{R_\theta}\big)_{c \to 0}$，有一系列 $\theta$，则由一系列的 $\big(\frac{K \cdot c}{R_\theta}\big)_{c \to 0}$，作 $\big(\frac{K \cdot c}{R_\theta}\big)_{c \to 0}$ 对 $\sin^2\frac{\theta}{2}$ 的曲线，截距 为 $\frac{1}{M_w}$，斜率 为 $\frac{16\pi^2 n^2}{3\lambda^2}\langle R_g^2\rangle$；
• 在固定浓度 $c$ 下测得的 $\frac{K\cdot c}{R_\theta}$ 值对 $\sin^2\frac{\theta}{2}$ 作图，得 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta \to 0}$，有一系列 $c$，则有一系列的 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta \to 0}$，作 $\big(\frac{K \cdot c}{R_\theta}\big)_{\theta \to 0}$ 对浓度 $c$ 的曲线，截距 为 $\frac{1}{M_w}$，斜率 为 $2A_2$

共混与溶液动力学：格子理论

理想气体的混合过程

理想气体模型将气体分子看作质点（有质量、无体积），分子间没有相互作用，严格遵循气体状态方程。

两种理想气体 $AB$ 在温度 $T$，压强 $p$ 下混合，混合过程的熵变为

$$\Delta S=\Delta S_A+\Delta S_B=n_AR\ln\frac{V_A+V_B}{V_A}+n_BR\ln\frac{V_A+V_B}{V_B}\tag{31}$$

其中，$n_A$ 表示 $A$ 组分的物质的量，$V_A$表示 $A$ 组分的体积，由摩尔分数的关系 $x_A=\frac{n_A}{n_A+n_B}$ 代换上式，可得

$$\Delta S_{mix}=-nR(x_A\ln x_A+x_B\ln x_B) \tag{32}$$

由于是理想气体，分子之间无相互作用，则

$$\Delta H_{mix}=0 \tag{33}$$

由此可得理想气体混合过程的吉布斯自由能变为

$$\Delta G_{mix}=\Delta H_{mix}-T\Delta S_{mix}=nRT(x_A\ln x_A+x_B\ln x_B)\tag{34}$$

理想溶液混合过程

理想溶液中各组分分子之间相互作用相同，溶质分子与溶剂分子混合时，无热效应，无体积变化，即 $\epsilon_{AA}=\epsilon_{BB}=\epsilon_{AB}$

将理想气体中的摩尔分数换为体积分数，即

$$\phi_A=\frac{n_A}{n_A+n_B}=x_A$$

混合前，$AB$ 组分状态数量为1，熵为0

$$S_0^A=S_0^B=k\ln 1=0\tag{35}$$

混合后

$$\Delta S_{f}=k\ln \Omega=-k[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\tag{36}$$

则混合过程的熵变为

$$\begin{split} \Delta S_{mix}&=-k[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\\ &=-k[n_A\ln\phi_A+n_B\ln\phi_B] \tag{37} \end{split}$$

由于是理想液体，混合过程焓变为0，则混合过程的吉布斯自由能变为

$$\Delta G_{mix}=nkT[\phi_A\ln\phi_A+\phi_B\ln\phi_B]\tag{38}$$

实际溶液的混合过程

实际溶液混合过程能量变化不可忽略

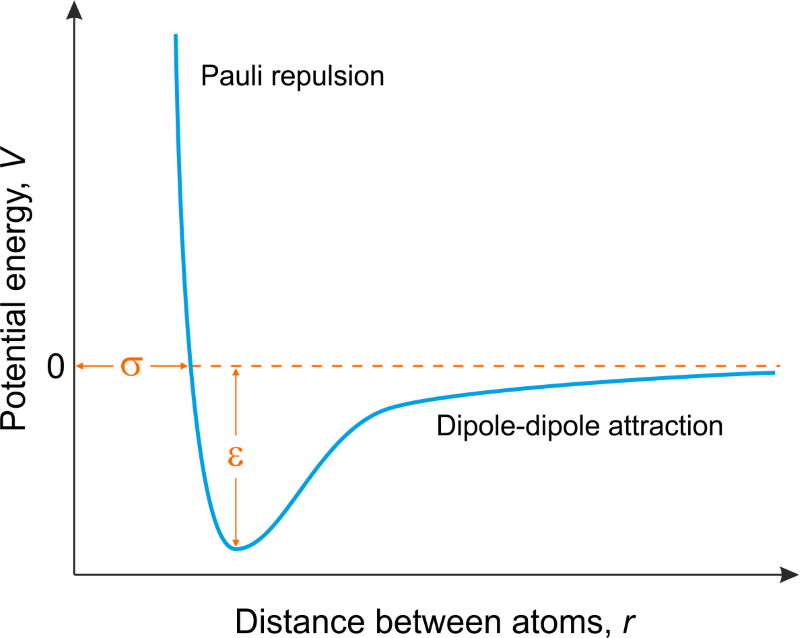
混合过程由格子理论易推得

$$\Delta E_{mix}=\frac{zn}{2}\phi_A\phi_B(2\epsilon_{AB}-\epsilon_{AA}-\epsilon_{BB})\tag{39}$$

其中$z$表示配位数，定义Folry-Huggins参数

$$\chi\equiv\frac{z}{2kT}((2\epsilon_{AB}-\epsilon_{AA}-\epsilon_{BB}))\tag{40}$$

则(39)式可以写为

$$E_{mix}=nkT\chi \phi_A \phi_B\tag{41}$$

• 当 $\chi<0$ 时，溶质倾向于溶解于溶剂中
• 当 $\chi>0$ 时，倾向于分相，即不溶解
• 当 $\chi=0$ 时，表现为理想溶液的特点

实际溶液混合过程中熵变与理想溶液一致，则混合过程的自由能变为

$$\Delta F_{mix}=\Delta E_{mix}-T\Delta S_{mix}=nkT[\phi_A\ln\phi_A+\phi_B\ln\phi_B+\chi\phi_A\phi_B]\tag{42}$$

高分子溶液与高分子共混

高分子共混中，每条分子链的自由能为

$$\frac{\Delta F_{mix}}{n/N}=kT[\phi_A\ln\phi_A+\phi_B\ln\phi_B+\chi N\phi_A\phi_B]\tag{43}$$

高分子溶液中，每个格点的自由能变化为

$$\frac{\Delta F_{mix}}{n}=kT[\frac{\phi_A}{N_A}\ln\phi_A+\phi_B\ln\phi_B+\chi\phi_A\phi_B]\tag{44}$$